
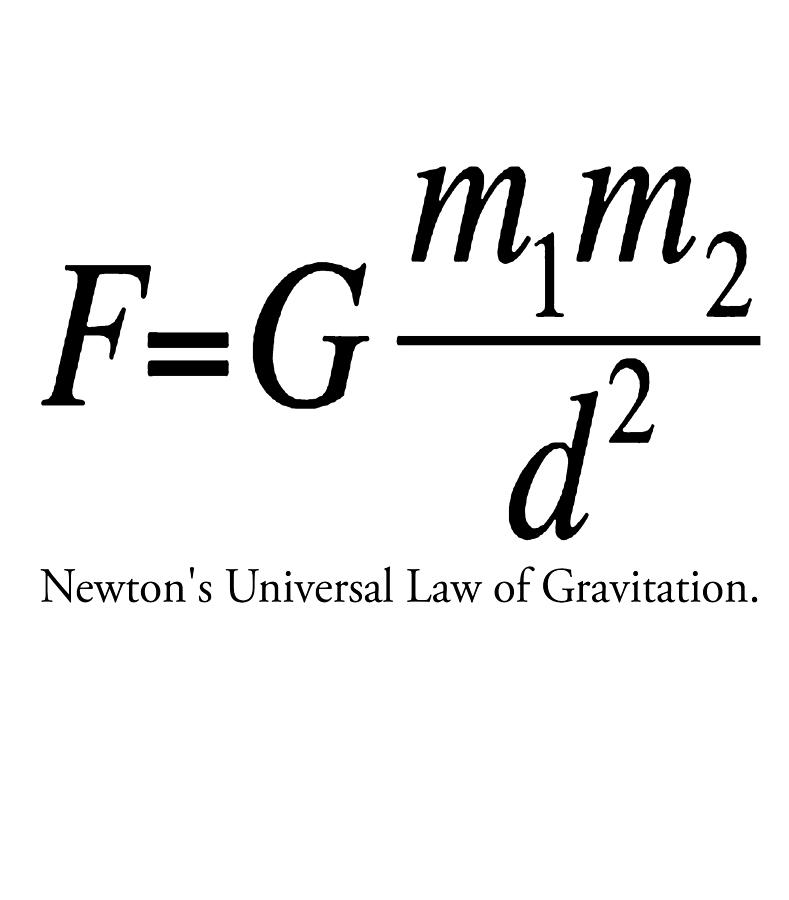
Newton proposed that, if you fired the cannonball with enough energy, it could fly all the way around the Earth and never land, because the Earth would be curving away underneath the ball at the same rate as the ball fell.

Fire the cannonball with more energy and it would land further away from the mountain, but it still would follow a curved trajectory in doing so. The ball would follow a curved trajectory as it moved forward and was attracted, by gravity, towards the ground at the same time. He used a thought experiment to explain his thinking: imagine you fired a cannonball horizontally from the top of a mountain on Earth. Newton concluded that the moon did feel the effect of the Earth's attractive force and that it was indeed falling towards Earth, but there was a very good reason why it didn't crash down. Which raised the question: if everything around the Earth should feel this force of attraction, including the moon, why doesn't our nearest neighbour fall and crash onto the surface of our planet in the same way as the apple did?

In fact, the attraction shouldn't even stop at the top of a tree but carry on way up into the heavens. The apple started in the tree and landed on the Earth, which means there must be a force of attraction between the apple and the Earth.Īnd even if the apple were higher up in the tree, it would still feel this force of attraction with the Earth, reasoned Newton. The story goes that Newton saw an apple fall to the ground and it made him wonder why the fruit always fell straight to the ground why did it not veer off to the left or right? According to his own laws of motion, anything that begins moving from a standing start is undergoing acceleration and, where there is acceleration, there must be a force. Newton filled in that gap by supposing there was a force acting between the bodies that were moving around each other. Kepler's laws explain how the planets moved around the sun but not why. By looking at the movement of Mars, Kepler had calculated that planets orbited the sun in elliptical paths and, in a kind of celestial clockwork, his three laws of planetary motion allowed astronomers to work out the position of the planets in the future based on data from past records. Stargazers had spent millennia cataloguing the positions of the stars and planets in the night sky and, by the 17th century, the German astronomer and mathematician Johannes Kepler had worked out the geometry of these movements. Newton came to the formula after studying the centuries of measurements from astronomers before him.


 0 kommentar(er)
0 kommentar(er)
